For the impatient

I hired Maksoda, a woman from India who just learned to use a computer, to scrape all of my old posts from around the web and put them together as a coherent set of markdown files. The old posts will be appearing here as if they were posted on the original date. The full set of archives are already available on my wiki. The first post she could recover was from 1998. I'm still trying to see if old copies of my .plan file still exist in some way on some old media I may still have sitting around.I'm slowly moving the archives to here as well. This is what computing was like for me at the turn of the century.

The history

I started to update my .plan file in 1986. It was a running list of random things I was doing and thinking at the time. I had a few accounts on UNIX shell servers around the US at the time, but the one many people started to finger was at Shore.net. This was the start of my writing down thoughts for a global audience.

In 1996, I upgraded the plan file to be html-enabled and then started to experiment with writing a web log. This is long before it was called blogging. Originally, I called it com.lewman. It was hosted on my own domain at lewman.com, but as I was experimenting with object oriented programming at the time, com.lewman seemed like a cooler name. The whole thing was managed by a set of bash scripts, which basically took a directory structure like YYYY/MM/DD/title.txt and turned it into a newest date first log of text on my website. This was great for 1996, but soon I realized it just looked like a set of bash scripts creating some basic html. Netscape and others started to have cooler websites, so I realized I needed something better. I learned PHP and decided to upgrade the scripts to it. Here's a sample of the code from July 1999. And yes, that was my desktop on Redhat 2 in 1999.

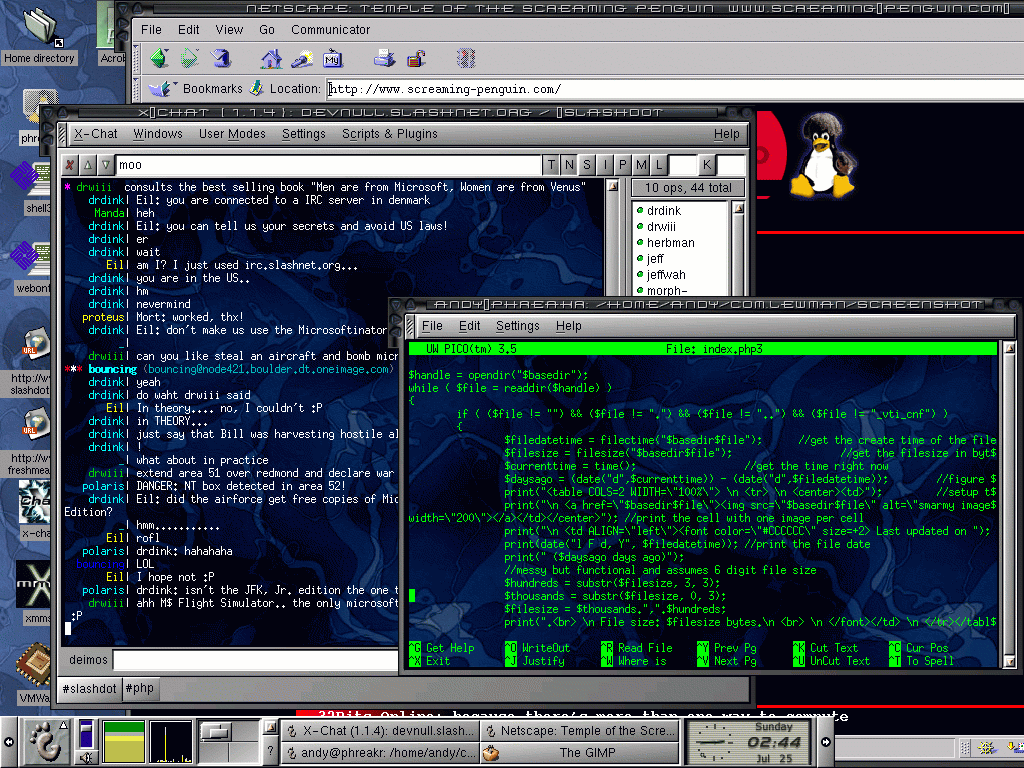
Learning PHP was sort of comical. I came from a decade of coding in assembly language and ANSI C. However, PHP seemed like the cool, new thing to learn, so I learned it. However, it worked for the web and was easier to manipulate HTML than bash, C, Perl or something else.

If you want a trip through memory lane for some of you, browse the screenshot directory. Enjoy the archives.